Traffic flow and pedestrian crowds are complex phenomena that describe various collective dynamics. In an increasingly urbanised society, their regulation poses critical safety and environmental challenges. This research aims to explore the application of stochastic port-Hamiltonian systems as an original and innovative paradigm for modelling pedestrian and vehicle dynamics.

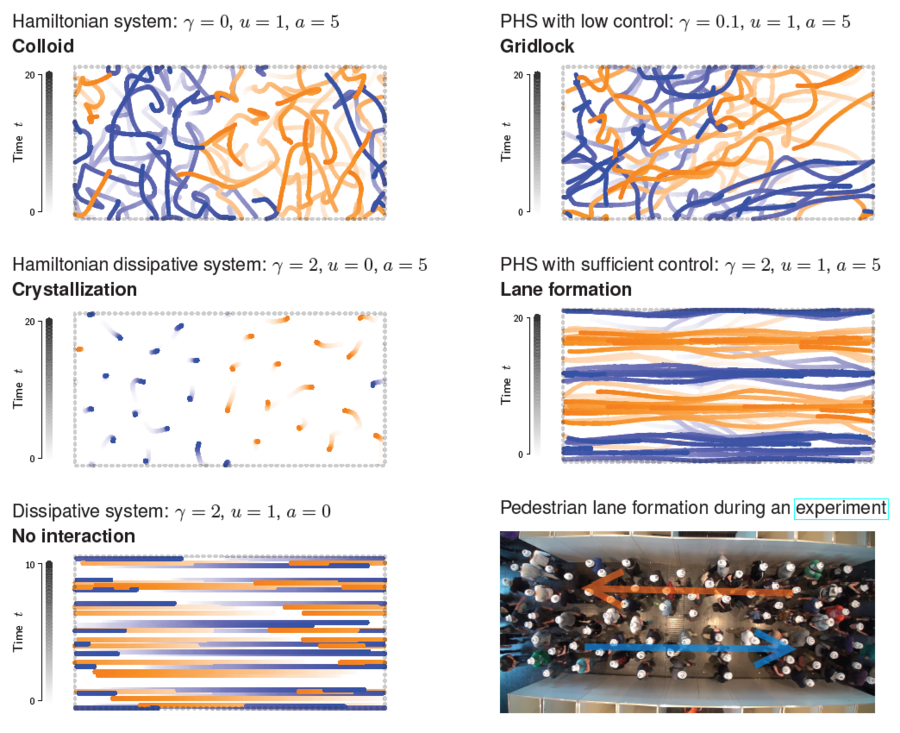
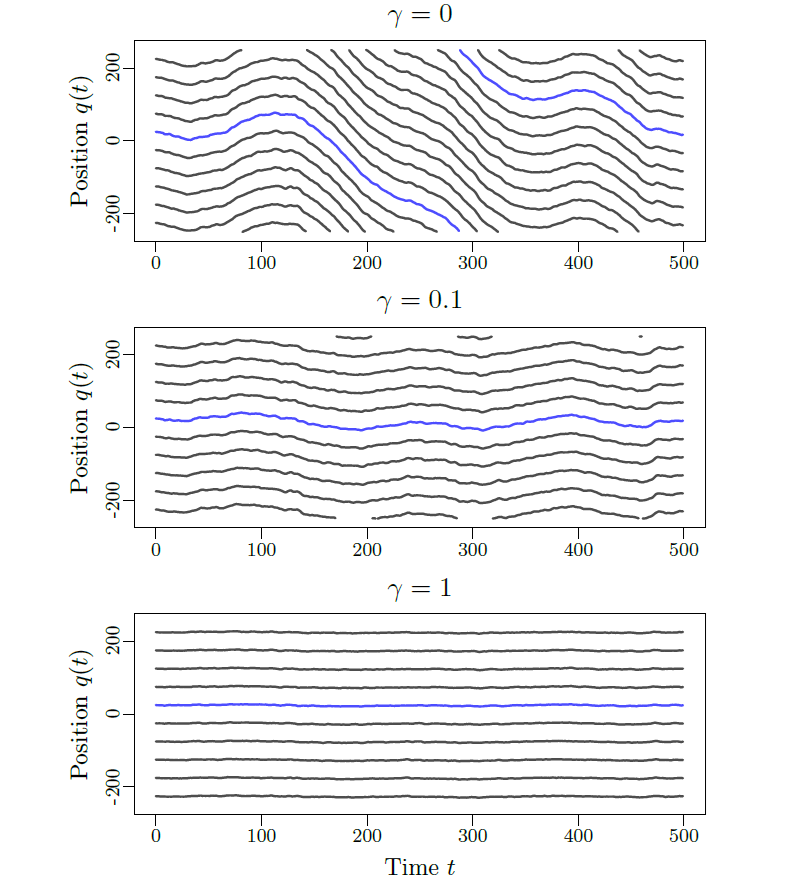
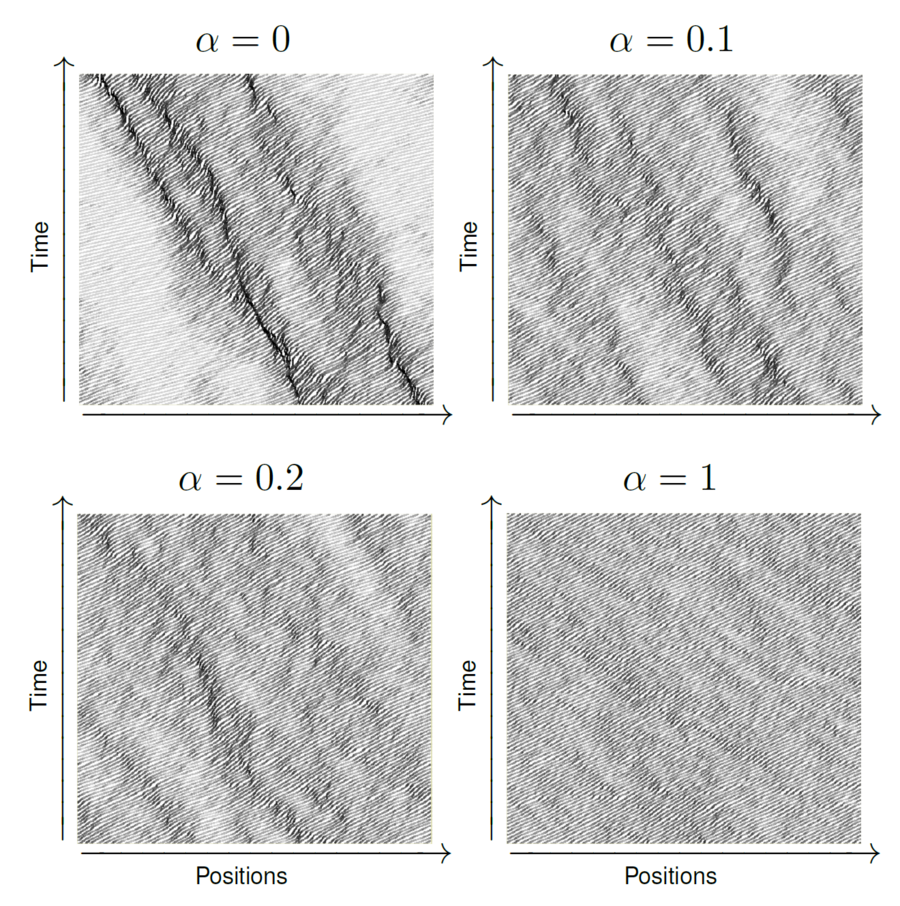
The port-Hamiltonian formulation not only enables control of vehicle or pedestrian dynamics through the ports but also provides a direct multiscale description using the Hamiltonian as a macroscopic order parameter. For certain parameter configurations, the Hamiltonian behaviour can be determined without the need for tedious computations of microscopic dynamics. Using the balance equation, we can leverage the Hamiltonian as a Lyapunov function to address system stability. Numerical investigations enhance our understanding of the connections between Hamiltonian behaviour and the emergence of collective dynamics, such as lane and stripe formation and stop-and-go waves.

Our objective is to establish, simulate, and analyse a novel class of linear and nonlinear stochastic port-Hamiltonian models of road traffic and pedestrian dynamics. In addition to the type and nature of the noise and stochastic components, the focus is on the input control and feedback terms, which can be state-dependent to incorporate adaptive behaviour, agent-specific to model group and leader dynamics, or again random to introduce further uncertainty. By systematically addressing these aspects, this research strives to contribute both to the development of advanced road traffic and pedestrian models and to applications of stochastic port-Hamiltonian systems.

One-dimensional port-Hamiltonian car-following model

Two-dimensional port-Hamiltonian pedestrian model